Math Tricks/Shortcuts
So, you want to do some math? Here are some tricks/shortcuts on calculating that *might* be helpful.
Index
- Easily Square a 2 digit number
- Easily Cube a 2 digit number
- Easily Square Root a 3-4 digit number
- Easily Cube Root a 1-6 digit number
- Easily Convert Fractions To Decimal
- Easily Calculate Area of irregular polygons
Easily Square a 2 digit number
Squaring is easy for 1 digit numbers, and is the same for 2 digits! How do you do 2 digit squares, the “fast” way, you might ask?
Well, you’ll need to look at this “formula” first:
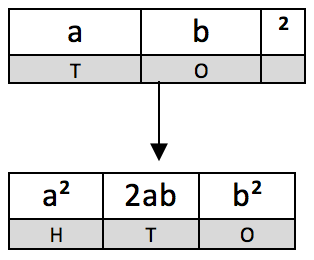
which is similar to this in algebra:
(a+b)² = a² + 2ab + b²
So according to the formula,
to find 43², just perform:
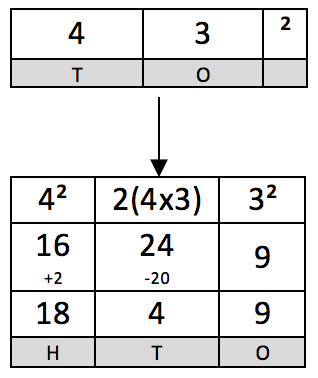
∴43² = 1849
Yay! Easy, right?
*”fast”: This method might be slower than the normal way. Unless you get the hang of counting quickly without “drawing” this ridiculous table out (which is easy, considering that 2-digit squares only create very small numbers).
Easily Cube a 2 digit number
Cubing is easy! If you’re lazy to calculate a 2 digit cube the “slow” way, here’s how to do it the “faster” way!
First, memorise this “formula”:
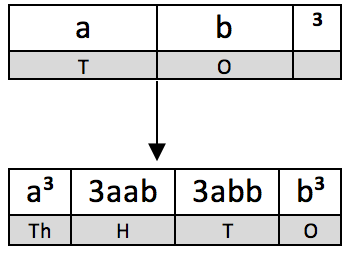
which is similar to this in algebra:
(a + b)³ = a³ + 3a²b + 3ab² + b²
So according to the formula,
to find 23³, just perform
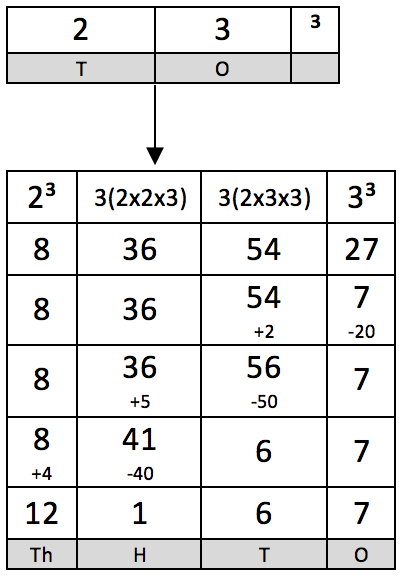
∴23³ = 12167
Voila! Easy, right?
*”faster”: Again, this might take longer than the normal way. Unless you can count in your head with speed and keep all numbers in memory, and not writing any of these out, which, I think most of you can’t (including me).
Easily Square Root a 3-4 digit number
You’ve learnt the shortcut to square! What about square rooting?
You probably know how to do 1-2 digit number square roots, but what about larger numbers?
Here is the method/shortcut! Follow this carefully:
To figure out
√1̅8̅4̅9̅
- Separate the value at hundreds place
- √1̅8̅|4̅9̅
- Figure out the nearest lower perfect square for the left section
- √1̅6̅|4̅9̅
- Find out its square root & remember the number
- √1̅6̅ = 4
- ∴ number = 4
- Next, figure out which of 2 numbers have the same last digit as the current value (unless its 5 or 0)
- 3² = 9 (same as 1849)
- 7² = 49 (same as 1849)
- Remember the numbers above:
- number = 3 or 7
- Write the 2 possible values from those numbers
- √1̅8̅4̅9̅ = 43 or 47
- Figure out which number is nearer.
- 43 ≈ 40
- 47 ≈ 50
- while
- 40² = 1600
- 50² = 2500
- 1849 is nearer to 1600,
∴ √1̅8̅4̅9̅ is nearer to 40,
∴ √1̅8̅4̅9̅ = 43
Easy, right?
*Pros: faster than manually counting
*Cons: only works with perfect squares
Easily Cube Root a 1-6 digit number
Now, how should you cube root numbers the fast way?
First, remember these cubes to solve cube roots from 1-3 digits:
0³ = 0
1³ = 1
2³ = 8
3³ = 27
4³ = 64
5³ = 125
6³ = 216
7³ = 343
8³ = 512
9³ = 729
And follow this method carefully for 4-6 digit cube roots:
To figure out
∛1̅2̅1̅6̅7̅
- Separate the value at thousands place
- ∛1̅2̅|1̅6̅7̅
- Figure out the nearest lower perfect cube for the left section
- ∛0̅8̅|1̅6̅7̅
- Find out its cube root & remember the number
- ∛0̅8̅ = 2
- ∴ number = 2
- Next, figure out which number have the same last digit as the current value
- 3³ = 27 (same as 12167)
- ∴ number = 3
- Finally, merge the numbers found from the above questions.
- ∛1̅2̅1̅6̅7̅ is equal to 23
∴ ∛1̅2̅1̅6̅7̅ = 23
Easy, right?
*Pros: faster than manually calculating
*Cons: only works with perfect cubes
Easily Convert Fractions To Decimal
Converting fractions to decimal is easy… if you know the tricks!
A quick note: this tutorial only teaches you how to figure out fractions as a decimal from 1/1 to 12/12. So let’s get to it.
Some fractions are easy:
1/1 = 1
1/2 = 0.5
1/4 = 0.25
1/5 = 0.2
1/8 = 0.125
1/10 = 0.1
Now, you might ask, what about the rest?
First, the denominator 3.
1/3 = 0.3333…
2/3 = 0.6666…
As you can see, there’s a pattern here, which is 0.3333… multiplied by the numerator.
Next! The denominator 6.
1/6 = 0.1666…
2/6 = 1/3 = 0.3333…
3/6 = 1/2 = 0.5
4/6 = 2/3 = 0.6666…
5/6 = 0.8333…
Well, this one I can’t help you, but you need to remember 1/6 and 5/6 yourself.
Next: the denominator 7.
Before we get to the fractions, remember the pattern: “142857”.
Let’s take a look:
1/7 = 0.142857142857…
2/7 = 0.2857142857…
3/7 = 0.42857142857…
4/7 = 0.57142857…
5/7 = 0.7142857142857…
6/7 = 0.857142857…
Here’s how to remember them:
– All numbers have a infinite decimal places with the pattern 142857.
– They start on a certain digit:
1/7 = 0.1.. (n + 0)
2/7 = 0.2.. (n + 0)
3/7 = 0.4.. (n + 1)
4/7 = 0.5.. (n + 1)
5/7 = 0.7.. (n+ 2)
6/7 = 0.8.. (n + 2)
*n = numerator
Okay, now look at denominator 9. This one’s easy:
1/9 = 0.1111…
2/9 = 0.2222…
3/9 = 0.3333…
4/9 = 0.4444…
5/9 = 0.5555…
etc.
Great! Now onto denominator 11. If you know the multiples of 9, you probably can solve this with ease:
1/11 = 0.090909…
2/11 = 0.181818…
3/11 = 0.272727…
etc.
Now the last one: denominator 12. Well you’ll need to memorize some:
1/12 = 0.0833… (5/6 ÷ 10)
5/12 = 0.4166… (2/3 + 1/12)
7/12 = 0.5833… (1/2 + 1/12)
11/12 = 0.9166… (1 – 1/12)
Others can be converted by simplifying.
***
That’s it! You can now convert fractions to decimal in lightning speed!
1/1 = 1
1/2 = 0.5
1/3 = 0.333…
1/4 = 0.25
1/5 = 0.2
1/6 = 0.666…
1/7 = 0.142857…
1/8 = 0.125
1/9 = 0.1111…
1/10 = 0.1
1/11 = 0.0909…
1/12 = 0.0833…
Easily calculate area of irregular polygons
This is by using the shoelace method.
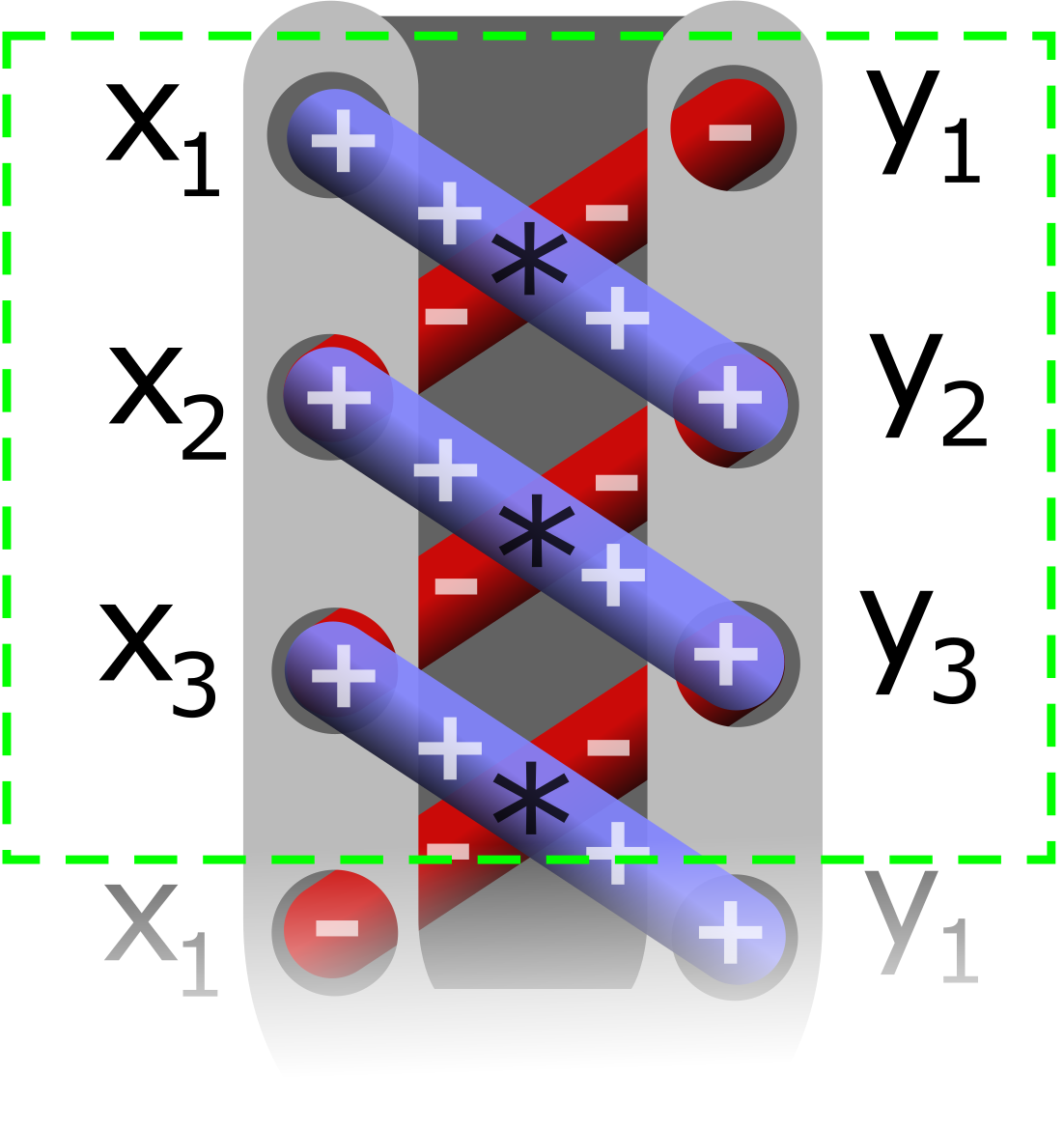
Area = |[(x1*y2+x2*y3+…+x(n-1)*yn+xn*y1)-(y1*x2+y2*x3+…+y(n-1)*xn+yn*x1)]|*1/2
The area formula is valid for any non-self-intersecting polygon, which can be convex or concave.
For those who don’t understand:
First, you’ll need to get coordinates for the polygon. We’ll need an example
Ok, a triangle of vertices (2,4), (3,−8), and (1,2), using the shoelace method,
List the coordinates in a matrix.
Then, draw diagonal lines to the bottom right like so:
Then get the sum of the products of the numbers. Eg:
(2 × −8) + (3 × 2) + (1 × 4) = −6
Now draw more diagonals in the opposite manner and repeat the process.
(4 × 3) + (−8 × 1) + (2 × 2) = 8
Now, to get the area, just calculate the difference of the sums:
|(−6)−( 8)| = 14
Then, divide that by 2!
(14)/2 = 7
Area = 7 unit2
Easy right?
